Fine-tuning Machine Learning Models with Additional Quantum Chemistry Data
Introduction
We have shown in a previous tutorial how a pre-trained DelFTa EGNN model [1] on the QMugs dataset [2] can be applied to predict the HOMO-LUMO gap of PCB molecules. The data points were placed in a classification diagram based on the HOMO-LUMO gap and the rotational angle between the two ring structures. A dioxin toxicity boundary was defined to classify if the PCB molecules were within this specific toxicity limit.
We also compared these DelFTa prediction results to the PubChemQC PM6 [3] HOMO-LUMO gap values and could identify outliers.
In this tutorial, we fine-tune the DelFTa EGNN on PubChemQC PM6 PCB molecule data to more accurately predict the HOMO-LUMO gap of PCBs and treat the outliers. We assume the values in the PubChemQC PM6 dataset (accessible via the MQS Search API) are closer to the true experimental values than the QMugs ones, since some values predicted by the DelFTa model (trained only on the QMugs dataset) showed large deviations from the rest of the data points as demonstrated in our previous tutorial.
Fine-tuning a DelFTa model with PCB data
To start, we will use the following MQS Search API query to grab 194 PCBs from the PubchemQC PM6 and QMugs datasets:
|
|
From the resulting PCB data, we only use PubchemQC PM6 data since the DelFTa model has already been trained with the QMugs dataset. As shown in the previous tutorial, we can extract the HOMO-LUMO gap value and the 3D atom coordinates of the molecules from this data.
We fine-tune the pre-trained DelFTa model using the atomic numbers, 3D coordinates of atoms, and bond information of each PCB. While it is not possible for us to remove the QMugs outlier datapoints from the model’s training without completely retraining it, we can still treat these outliers solely by fine-tuning; we chose a learning rate of 2.0 * 10-3 to strike a balance between giving weight to the PubchemQC PM6 PCB datapoints while also retraining the model’s original QMugs training to a good extent.
Model prediction performance comparison
We ran predictions with the fine-tuned DelFTa model on all 194 PCB molecules, and compared the results to the HOMO-LUMO Gap values from the PubChemQC PM6 data. This is shown in Figure 1, in which the x-axis represents different PCB molecules, and the y-axis represents HOMO-LUMO gap values in electronvolt (eV):
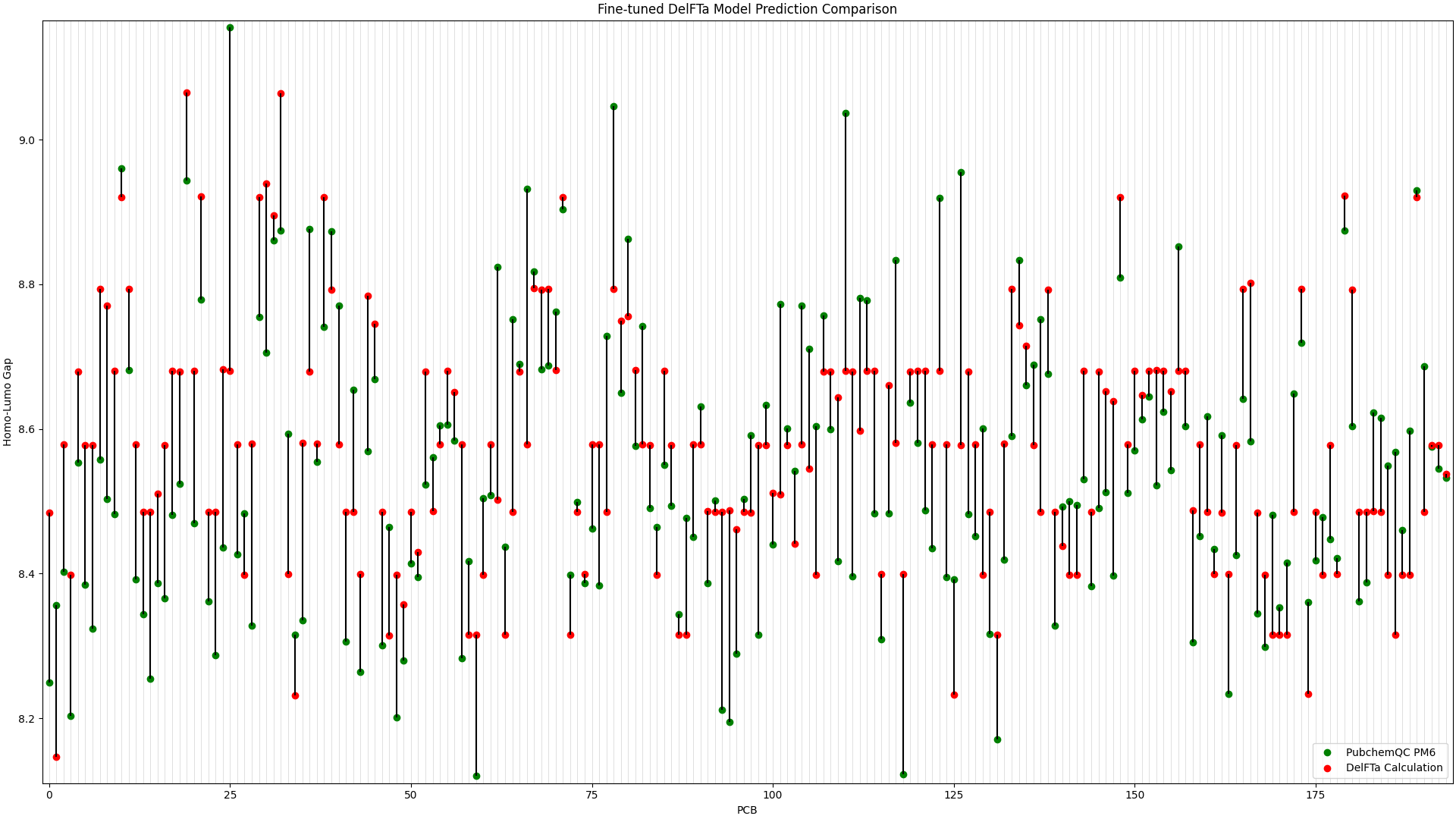Figure 1: Fine-tuned DelFTa Model Predictions
To illustrate the improvement in the above picture with the fine-tuned DelFTa model, we can compare the above figure to the predictions from a pre-trained DelFTa model:
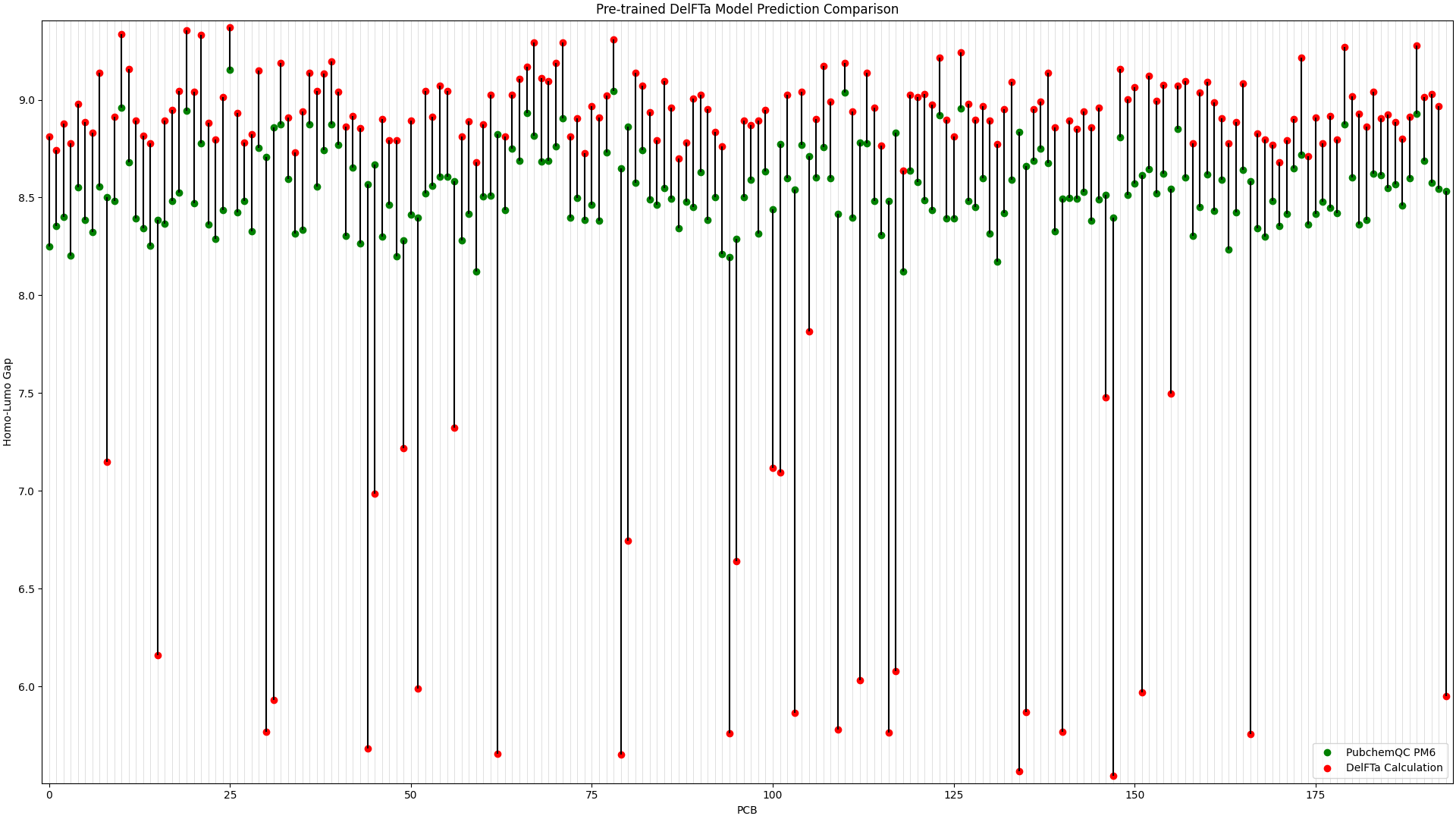Figure 2: Pre-trained DelFTa Model Predictions
As you can see in Figure 1 (note that the y-axis scale is different from Figure 2), the pre-trained DelFTa model had numerous outliers in prediction in which the model underpredicted (in contrast to it overpredicting otherwise) and was off by well over 1eV, however these outliers are not seen in Figure 2 with the fine-tuned model.
In terms of accuracy, in our test data of 39 molecules (none of which were outliers) that we did not fine-tune the model with, the pre-trained DelFTa model had a mean absolute error of 0.41 eV, while the new fine-tuned model has significant improvement with a mean absolute error of 0.11 eV.
Note that the 100 PCBs analyzed in the previous tutorial are a subset of the 194 displayed here.
Clearly, training a DelFTa with PubChemQC PM6 PCB data improved its ability to predict the HOMO-LUMO gaps of PCBs. To demonstrate model fine-tuning and prediction in a lightweight manner, we did use a small dataset of 194 molecules in this experiment, but the same procedure can be applied to more extensive datasets for other experiments as well.
We hope we showed you that combining the DelFTa model together with an additional dataset for fine-tuning can be of value for interesting machine learning studies with molecular quantum information.
You are always welcome to reach out if you have any feedback, questions, ideas or even collaboration projects to push this kind of work and research further (contact (at) mqs [dot] dk).
References
[1] K. Atz, C. Isert, M. N. A. Böcker, J. Jiménez-Luna & G. Schneider; Δ-Quantum machine learning for medicinal chemistry; ChemRxiv (2021); http://doi.org/10.26434/chemrxiv-2021-fz6v7-v2
[2] C. Isert, K. Atz, J. Jiménez-Luna & G. Schneider; QMugs, quantum mechanical properties of drug-like molecules; Sci Data 9, 273 (2022); https://doi.org/10.1038/s41597-022-01390-7
[3] M. Nakata, T. Shimazaki, M. Hashimoto, and T. Maeda; J. Chem. Inf. Model. 2020, 60, 12, 5891–5899; PubChemQC PM6: Data Sets of 221 Million Molecules with Optimized Molecular Geometries and Electronic Properties; https://doi.org/10.1021/acs.jcim.0c00740