Introduction

Over the last decades researchers have developed quantum chemistry models ranging from ab-initio methods such as density functional theory (DFT) to semi-empirical methods such as PMx and GNFx-xTB. These methods can be used to calculate quantum properties of molecules. By using these methods to perform high-throughput screening over hundred thousands to millions of molecules, the results of these calculations have been collected into various datasets in recent years, for example the PubChemQC PM6 [1] which mined data from PubChem or QMugs based on the ChEMBL database [2]. This blog article presents how these quantum chemistry datasets can be leveraged in combination with machine learning (ML) methods to retrieve valuable insights.

Aryl hydrocarbon receptor (AhR, dioxin receptor)

The Aryl Hydrocarbon Receptor (AhR), commonly referred to as the dioxin receptor, is a vital protein encoded by the AHR gene in humans. It functions as a transcription factor, playing a crucial role in regulating gene expression. AhR belongs to the PAS (Per-Arnt-Sim) superfamily of receptors, which are responsible for responding to various environmental stresses like hypoxia and circadian rhythm. Moreover, they also exert control over fundamental physiological processes such as vascular development, learning, and neurogenesis, highlighting the receptor’s multifaceted functions [3].

AhR exhibits a remarkable capacity to integrate diverse signals from the environment, diet, microbiota, and metabolism to orchestrate complex transcriptional programs [4]. This integration occurs in a manner that is specific to the ligand, cell type, and overall context. Consequently, AhR’s regulatory activities are highly versatile and tailored to specific biological contexts. However, studying the effects of AhR agonists and other chemicals has traditionally relied on assays involving biomaterials, a process that can be time-consuming with in-vitro experiments.

To better understand the intricate workings of AhR and assess the toxicity of AhR agonists and other chemicals, researchers are actively exploring alternative methods that reduce the need of animal experiments and decrease research duration on biomaterial-based assays [5,6,7,8]. These advances have the potential to accelerate toxicological research, facilitating the development of safer and more environmentally friendly chemical compounds.

Polychlorinated biphenyls (PCBs)

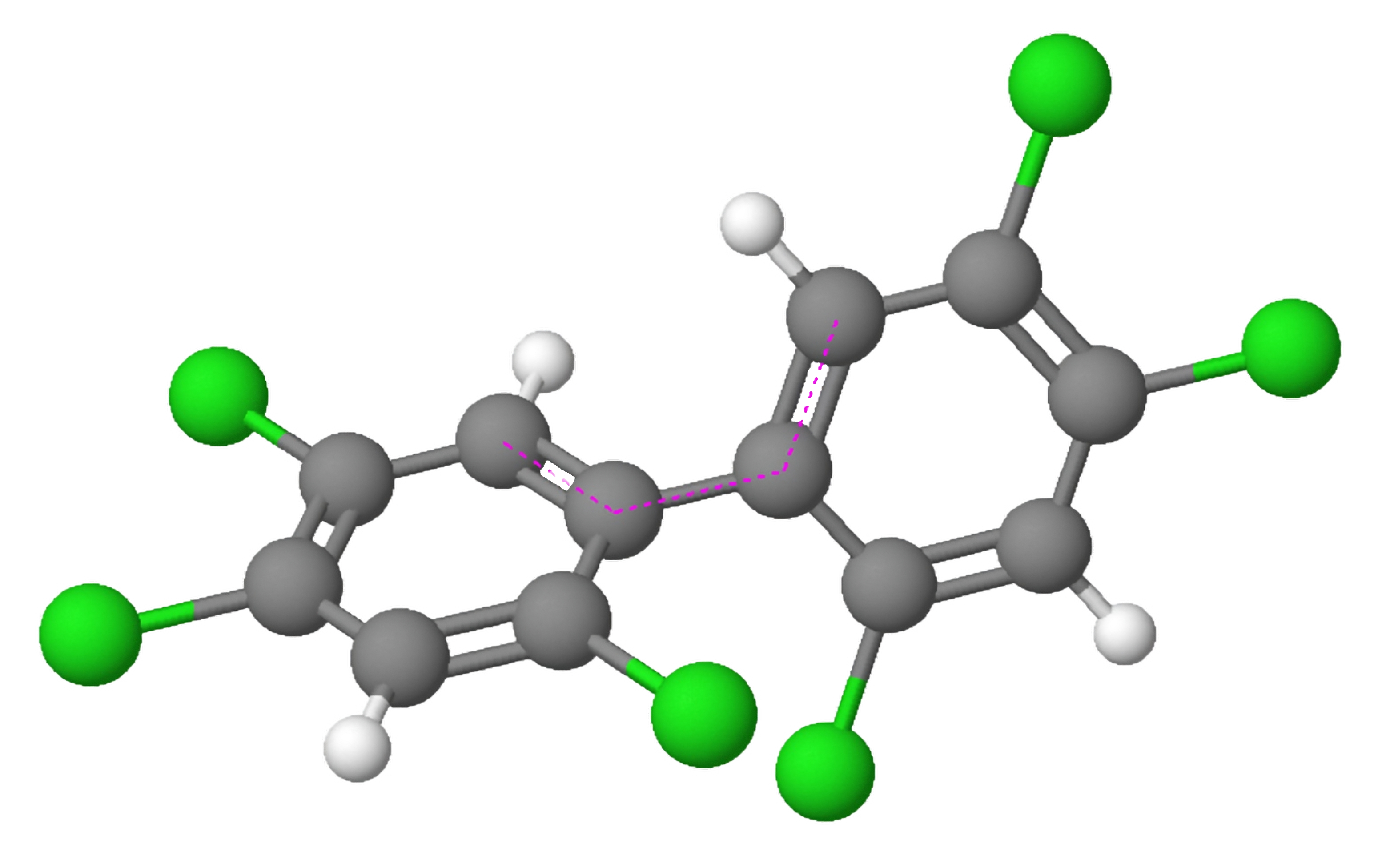
Figure 1: 3D model of a polychlorinated biphenyl.

Polychlorinated biphenyls (PCBs; Figure 1) encompass a collection of synthetic organic chemicals that were once extensively utilized in both industrial and consumer products. However, their ban in the 1970s stemmed from their harmful effects on health and their ability to persist in the environment. The AhR, a protein found in various cell types throughout the body, plays a pivotal role in the metabolism of numerous drugs and environmental toxins, including PCBs. Activation of the AhR by PCBs initiates alterations in gene expression, which can elicit a broad range of physiological effects.

The toxicity of PCBs is contingent upon the arrangement of chlorine atoms substituted on the phenyl rings [5]. Within this group, there exists a subset of 12 PCBs called non-ortho- or mono-ortho-chlorinated PCBs, which exhibit AhR-related activities akin to those observed in dioxins.

Toxicity in similar molecules can be inferred by examining the energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied orbital (LUMO) [9]. A larger energy gap implies greater stability of the molecule concerning reactions with biomolecules.

The relative stability of highly chlorinated PCBs, coupled with their increased lipophilicity, leads to their widespread distribution across diverse environments, followed by prolonged accumulation within wildlife and human populations. Despite previous extensive studies, accurately determining the toxicity of PCBs remains a challenge. Consequently, PCBs serve as ideal candidates for testing models aimed at assessing the toxic and bioaccumulative behaviours of AhR agonists.

HOMO-LUMO gap as a toxicity indicator

Molecular orbitals, such as HOMO and LUMO, represent wave functions that describe the distribution of electrons within a molecule. Composed of atomic components derived from constituent atoms, the HOMO and LUMO exhibit distinct energy levels. The energy difference between these two orbitals is referred to as the HOMO-LUMO gap. The HOMO-LUMO gap is expressed in electronvolts (eV), a unit of energy commonly used to quantify small energy amounts. The magnitude of the energy gap can vary among different molecules. A small gap, below a certain threshold, is considered a necessary condition for molecules to possess significant potency.

The assessment of the HOMO-LUMO energy gap allows to determine the toxicity of PCBs. Below the threshold of 4.87 eV are the 12 dioxin-like PCBs, while above the threshold are non-dioxins. In the context of PCBs, the potency of AhR-mediated effects serves as a distinguishing factor between dioxin-like and non-dioxin-like molecules. However, it is important to note that the assessment of toxicity within the dioxin-like subgroup requires consideration of additional factors. While the HOMO-LUMO energy gap provides an overarching indicator of PCBs’ toxicity, it does not provide the sole determinant [5].

Torsional angle

The torsional angle (Figure 2) refers to the spatial configuration of atoms in a molecule, specifically the angle formed by the rotation of one group of atoms around a bond axis with respect to another group. The torsional angle, which is crucial in determining the overall shape and stability of a molecule, varies among different molecules depending on their structural arrangement, and play a significant role in understanding and predicting the behaviour of a molecule, as the magnitude of these angles directly affects molecular properties such as conformational stability, reactivity, and intermolecular interactions. Torsional angles arise due to the presence of rotatable bonds and can be quantified using the degree of rotation.

The torsional angle in a PCB molecule can impact their interaction with the aryl hydrocarbon receptor (AhR). The conformational change caused by the torsional angle can modulate the binding affinity and activation of AhR by PCBs, ultimately influencing their toxicological effects [5].

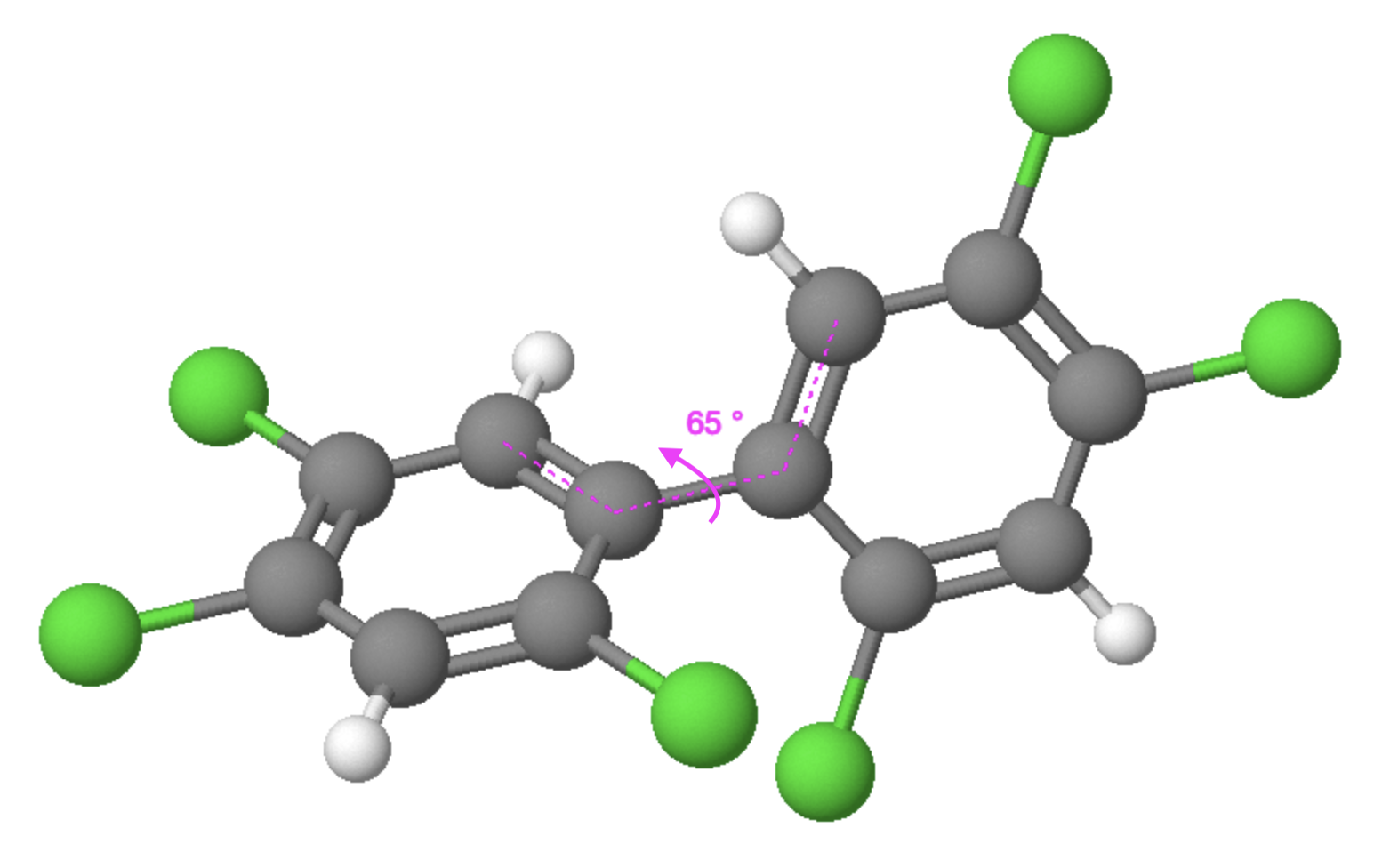
Figure 2: Torsional angle of a PCB molecule

PubchemQC PM6

The PubChemQC PM6 dataset is a collection of electronic properties of 221 million molecules with optimized molecular geometries [1]. The electronic properties were calculated using the PM6 method. The dataset covers 94.0% of the original PubChem dataset with respect to neutral molecules, making it a valuable resource for researchers in the field. How to access the dataset via the MQS Search UI and API can be read up on in the first Search API tutorial: MQS Search API Part 1 Tutorial.

QMugs dataset

The QMugs (Quantum-Mechanical Properties of Drug-like Molecules) dataset contains optimized molecular geometries calculated via density functional theory (DFT), thermodynamic data calculated with the semi-empirical method GFN2-xTB, atomic and molecular properties calculated with both DFT (ω B97X-D/def2-SVP) and GFN2-xTB.

The collection of QMugs consists of over 665,000 molecules that are biologically and pharmacologically significant. These molecules have been obtained from the ChEMBL database [8].

The dataset presented has multiple potential applications as highlighted in the QMugs research paper [8]:

• It can offer researchers a larger dataset that can be utilized to predict quantum chemical properties or establish correlations between the GFN2-xTB and ωB97X-D/def2-SVP levels of theory.
• It can aid in the advancement of machine learning techniques for generating molecular conformations and predicting molecular properties.
• It can support the development of deep learning frameworks that can predict quantum mechanical wave functions in atomic orbitals.
• It can facilitate research on quantum featurization in the context of pharmacologically relevant biological data.

The QMugs dataset features DFT-level properties and is found to have larger molecular samples and a larger number of distinct molecules than the QM9 (http://quantum-machine.org/datasets/) and ANI-1 (https://github.com/isayev/ANI1_dataset) datasets. It provides multiple conformers per molecule, enabling the training of QML models that can differentiate between molecular constitution and conformation. QMugs also provides a wide range of properties on multiple levels of theory and includes mostly compounds not previously reported in other DFT data collections.

Important to acknowledge is that the QMugs dataset holds a very limited number of PCBs compared to the PubchemQC PM6 dataset and has therefore implications for the machine learning model which is going to be presented in the next section. The Search API tutorial part 2 also holds some more information about the QMugs dataset: https://blog.mqs.dk/posts/getting_started_search_api_part2/

DelFTa toolbox

The DelFTa toolbox [9] is an open-source model that has been trained with the QMugs dataset to predict quantum-mechanical properties of drug-like molecules. The toolbox uses PyTorch modules and libraries, the Open Babel library, Numpy and JSON to define and run various models and tasks. The application provides a command-line interface in order to predict molecular properties from a SMILES string or a molecule file. The output results are provided either as JSON or CSV files.

DelFTa can predict a wide array of quantum observables on the molecular, atomic, and bond levels. Some of the properties that DelFTa can predict are:

• Formation energies: The energy required to form a molecule from its constituent atoms.
• Energies of HOMO and LUMO: Energies of the highest occupied and lowest unoccupied molecular orbital. These are important for understanding the electronic structure of molecules.
• HOMO/LUMO gaps: The energy difference between the HOMO and LUMO orbitals.
• Dipole moments: A measure of the separation of positive and negative charges in a molecule.
• Mulliken partial charges: A way to partition the electron density in a molecule among its constituent atoms.
• Wiberg bond orders: A measure of the strength of covalent and non-covalent chemical bonds.

The DelFTa toolbox applies an equivariant graph neural network with a message-passing layer.

Graph Neural Networks (GNNs) are neural networks specifically designed to operate on graph-structured data. Equivariant Graph Neural Networks (EGNNs) are an extension of GNNs that aim to capture and preserve symmetries present in the input graph data applying equivariant operations. In the context of graphs, symmetry refers to the invariance of the graph structure and its features under transformations such as rotations, translations, or permutations of the nodes. This can lead to several advantages, including better generalization to unseen data, improved robustness to noise and perturbations, and more efficient learning by leveraging the inherent structure and patterns of the data.

A message-passing layer facilitates information exchange and aggregation between connected nodes, enabling nodes to update their representations based on messages received from neighboring nodes. This enabling effective modeling of relational structures and improving the network’s ability to learn from graph-structured data.

The current version of the DelFTa toolbox only supports Python 3.8.X and 3.9.X versions of Linux builds.

The following points summarize the recommended installation steps for a conda environment:

1. The DelFTa toolbox can be cloned from its offical GitHub repository.

2. Create the Python environment with required installations using the environment.yml file. This can be done using conda env create -f environment.yml in the downloaded repository directory. After submitting this command, a conda environment named delfta will be created. The environment can be activated by using the conda activate delfta command.

3. The DelFTa toolbox can also be installed on a prepared environment by running the python setup.py install --user command in the DelFTa repo directory.

4. To get required files that include trained DelFTa model* and XTB utils, run: `python -c “from delfta.download import _download_required; _download_required()".

*To download additional models which were trained on different training set sizes, follow this download link provided by ETH Zurich.

In the following we are now going to compare the HOMO-LUMO gap data obtained from PubchemQC PM6, QMugs and via the DelFTa toolbox.

Get HOMO-LUMO gap data by using the MQS Search API

We are going to use the MQS Search API to get HOMO-LUMO gap data of PCBs stored in the PubchemQC PM6 dataset.

As explained in detail in the MQS Search API Part 1 Tutorial, we will start with getting our token to be able to reach the database via the Search API. The token can be obtained with your MQS Dashboard email and password as described in the Part 1 Tutorial.

On the molecule search page (Figure 3) we provide a documentation of the Search API.

Figure 3: “Search for chemicals (via API) tab on the molecule search page in the MQS Dashboard”

Now you can prepare a search query to search for the PCBs:

1
2
3

query = "PCB AND C12* NOT formula:*S NOT formula:*N* NOT formula:*O"

data = requests.get(f"{api_url}/search", params={"q": query}, headers=headers).json()

1
2
3
4
5
6
7
8

for pcb in data["response"]["docs"]:

    # Molecule ID:
    pcb_id = pcb["id"] 
    # SMILES code of molecule:
    SMILES = pcb["isomeric_smiles"]

    pcb_props = requests.get(f"{api_url}/compound/{pcb["id"]}", headers=headers).json()

To select the HOMO-LUMO gap, we choose S0 as the molecule state and the alpha register as the energy property. The 3d coordinates information is also being stored in a new array for later use:

1
2
3
4
5
6
7
8

for pcb_state in pcb_props["pubchemqc_pm6"]:
    if pcb_state["state"] == "S0":

        # Get HOMO−LUMO gap:
        HOMO_LUMO_Gap = pcb_state["properties"]["energy"]["alpha"]["gap"]
        
        # Get 3D geometry with shape of (<Number_of_Atoms>, 3):
        coords = np.array(pcb_state["atoms"]["coords"]["3d"]).reshape(-1, 3)

We have now accessed specific data from QMugs and this is an example what the data for one PCB holds:

• PCB Name: 2,3,3’,5-Tetrachlorobiphenyl
• SMILES Code: C1=CC(=CC(=C1)Cl)C2=CC(=CC(=C2Cl)Cl)Cl
• HOMO−LUMO Gap Value: 6.574814855781
• 3D Atom Coordinates: Array(shape:(Number_of_Atoms, 3))

Predicting the HOMO-LUMO gap by using DelFTa

Now we are going to predict the HOMO-LUMO gap value of a PCB by applying the DelFTa toolbox with the SMILES strings and the 3D atom coordinates data that we have collected.

Create an Open Babel Molecule Object from the SMILES string of the PCB and add hydrogen atoms:

1
2
3
4

from openbabel.pybel import readstring

mol = readstring("smi", SMILES)
mol.addh() # Adds Hydrogen atoms.

Pass 3D coordinates of atoms to the molecule object:

1
2
3

for atom, coord in zip(mol.atoms, coordinates):
    x, y, z = coord
    atom.OBAtom.SetVector(x, y, z)

Predict the HOMO-LUMO gap via DelFTa:

1
2
3
4
5
6
7

from delfta.calculator import DelftaCalculator

# Prepare DelFTa Calculator:
calc = DelftaCalculator(addh=False)

# Make predictions:
preds = calc.predict(mol)

The DelFTa prediction function will return a Python dictionary of the predicted values:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

{'wbo':
[{'0-1': 1.4635928285108784, '0-3': 0.11247402231651216, '0-5': 1.4651485560975337, '0-16': 0.9307198423872055, '1-2': 1.416853712718369, '1-17': 0.931873304102257, '2-3': 1.410260321460608, '2-5': 0.10810251813581974, '2-7': 1.0212926424278403, '3-4': 1.447762294545536, '3-18': 0.9264065040542494, '4-5': 1.4439071195028848, '4-6': 1.2419898643430511, '5-19': 0.9298978451088848, '7-8': 1.4107464260690588, '7-12': 1.3855066583460698, '8-9': 1.4394256891469703, '8-20': 0.924661022763001, '9-10': 1.4439716051888596, '9-15': 1.251288105013964, '10-11': 1.4389150192484086, '10-21': 0.9227660093041355, '11-12': 1.4176788092449024, '11-14': 1.2569783603366196, '12-13': 1.2456382012974325}],

'E_form':
array([-4.0662913], dtype=float32),

'charges':
[array([-0.01280808, -0.00144799, -0.01410628,  0.0281181 ,  0.03468447, 0.0072453 , -0.08946717, -0.00093684,  0.00319889,  0.04281836, 0.0217519 ,  0.0199199 ,  0.03606375, -0.03929779, -0.05472087, -0.07673271,  0.02948804,  0.01668386,  0.01211333,  0.01979109, 0.0190095 ,  0.02159348])],

'E_homo':
array([-0.32399112], dtype=float32),

'E_lumo':
array([0.00836667], dtype=float32),

'E_gap':
array([0.33245534], dtype=float32),

'dipole':
array([1.9053881], dtype=float32)}

Convert the predicted HOMO-LUMO gap value from Hartree to Electronvolt (eV) unit (DelFTa returns HOMO-LUMO gap value as Hartree in a dictionary so we need to multiply by Hartree-eV constants):

1
2
3
4

from scipy.constants import physical_constants

hartree_to_ev = physical_constants['Hartree energy in eV'][0]
HOMO_LUMO_Gap = preds["E_gap"].item() * hartree_to_ev

Calculation of the torsional angle

To calculate the torsional angle of a PCB, we need to apply the following steps:

Create a molecule object from the SMILES string with RDKit:

1
2
3
4

from rdkit import Chem

# RDKit Molecule Object:
mol = Chem.MolFromSmiles(SMILES)

Create a conformer object and pass atom coordinates to the object:

1
2
3
4
5
6

# RDKit Conformer Object:
conf = Chem.Conformer(mol.GetNumAtoms())

# Pass coordinate information of atoms to molecule conformation:
for indx, coord in enumerate(PCBs[pcb_name]["3DCoords"]):
    conf.SetAtomPosition(indx, coord)

To find the torsional angle between two benzene rings of a PCB, we need to first locate the benzene rings in the molecule and determine the bond that connects the two rings. Then we need to identify the bond atoms consisting of two atoms and a neighbor atom on a ring for each bond atom. Finally, we have now defined the bond atoms between the rings and the benzene ring atoms as the two planes to calculate the torsional angle.

1
2
3
4
5

# Create a two benzene template:
query = Chem.MolFromSmarts('c1ccccc1-c1ccccc1')

# Find atom indices of planes using template:
atom1, atom2, atom3, atom4 = mol.GetSubstructMatches(query)[0][4:8]

As an example atom1, atom2, atom3, atom4 variables will be equal to atom indices 2, 1, 9, 10 on Figure: Benzene bridge of hexachlorobiphenyl.

1
2
3
4
5

from rdkit.Chem import rdMolTransforms

# Calculate Torsional angle between
# atom1, atom2 vector plane and atom3, atom4 vector plane:
angle = rdMolTransforms.GetDihedralDeg(conf, atom1, atom2, atom3, atom4)

As an example, angle variable will be equal to 59.2896 degrees for the PCB molecule of Hexachlorobiphenyl.

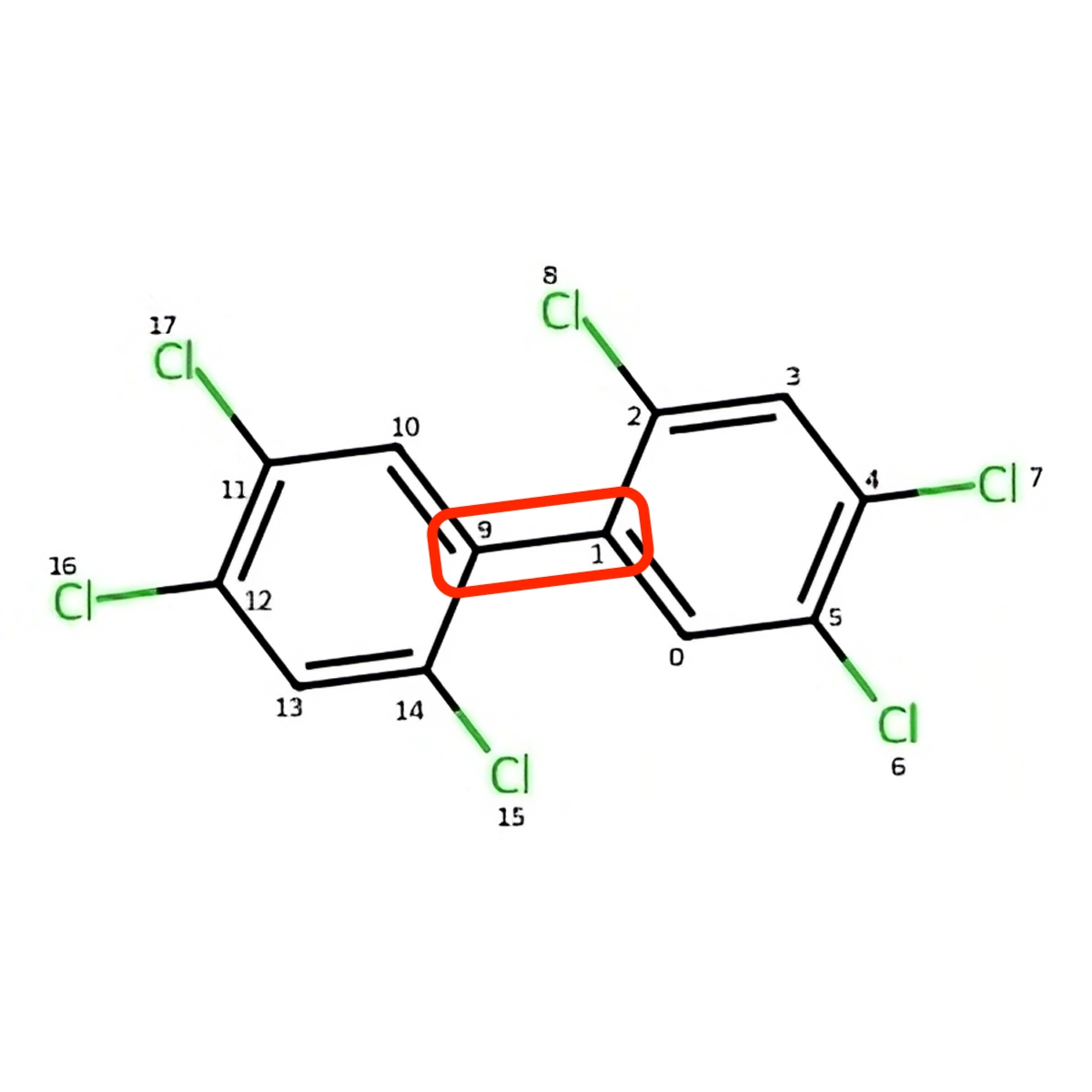
Figure 4: Benzene bridge of Hexachlorobiphenyl

Counting PCB Ortho Configurations

Locating the number of ortho configurations of a PCB we need to match ortho substructures:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

# Create RDKit Molecule Object using SMILES code of the PCB:
mol = Chem.MolFromSmiles(SMILES)

# Prepare ortho template:
ortho_template = "[*]c1ccc([*])c([*])c1"
query = Chem.MolFromSmarts(ortho_template)

# Find and count ortho groups:
ortho_groups = mol.GetSubstructMatches(query)
num_orthos = len(ortho_groups)

As an example, the num_orthos variable (number of orthos) will be equal to 8 for the PCB molecule of Hexachlorobiphenyl.

In next section, we will call molecules without any ortho group non-ortho structures , molecules that only have one ortho group will be defined as mono-ortho PCBs, and molecules that have two or more ortho group will belong to the class of multi-ortho PCBs.

Comparison and Results

The comparison of HOMO-LUMO gap values from the PubchemQC PM6 dataset and DelFTa predictions, we prepared a figure with 100 different PCBs (Figure 5) and their respective HOMO-LUMO gap values.

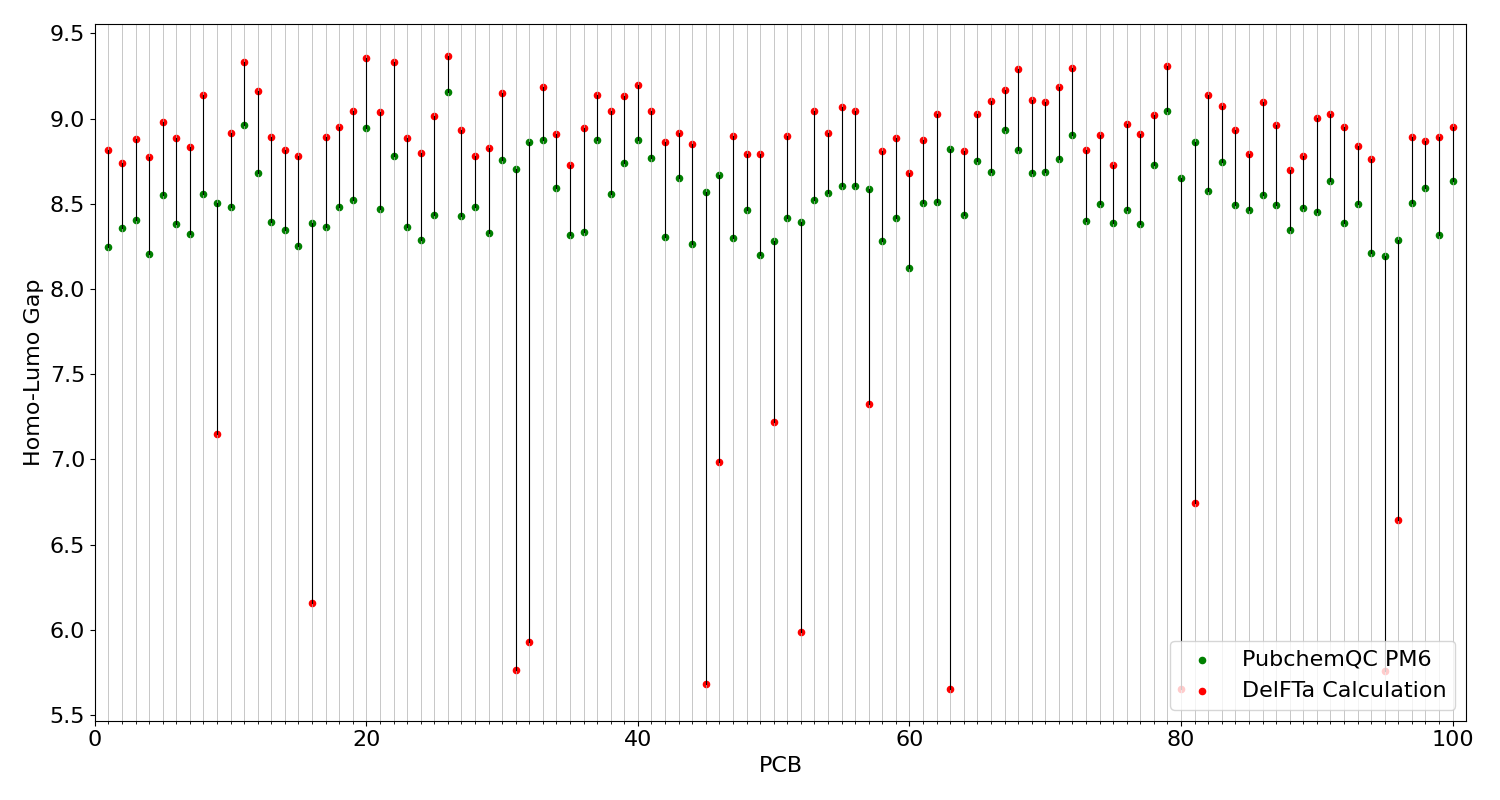
Figure 5: Comparison of HOMO-LUMO gap calculations.

On this figure the x-axis represents different PCB molecules, y-axis represents HOMO-LUMO gap values as electronvolt (eV). Red dots represents DelFTa prediction and green dots represents PubchemQC PM6 dataset values of HOMO-LUMO gap of PCB projected on x-axis. Dark black lines between red and green dots represent the difference of HOMO-LUMO gap values of PubchemQC PM6 dataset and DelFTa predictions.

We did also plot HOMO-LUMO gap values of the PubchemQC PM6 dataset and DelFTa predictions for a HOMO-LUMO gap versus torsional angle representation (Figure 6 and 7) which allow to visualize the toxicity threshold together with torsional angle and the HOMO-LUMO gap values. In this way one can identify if a molecule lies below the toxicity threshold or above.

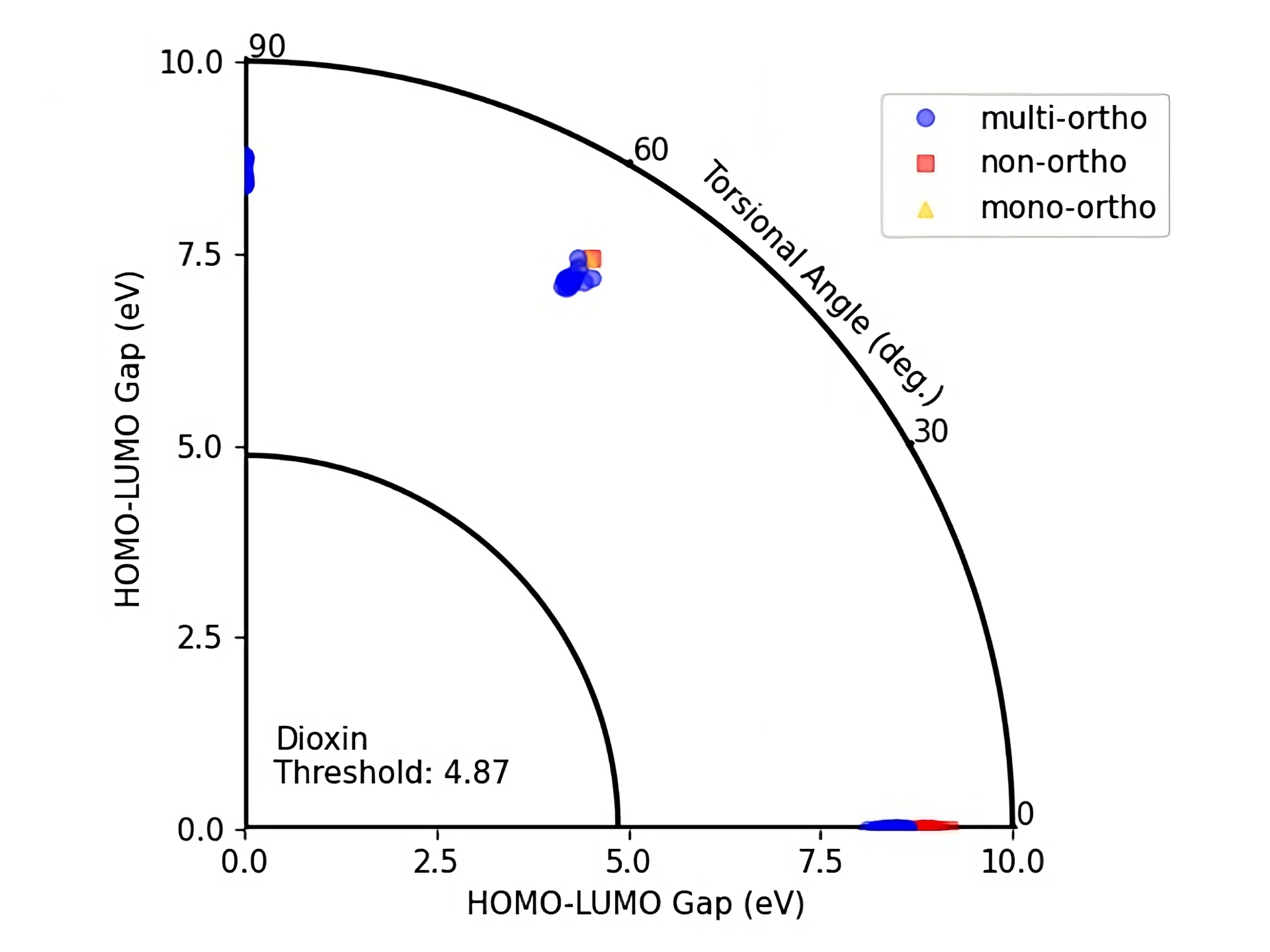
Figure 6: HOMO-LUMO gap - Torsional angle representation of PubchemQC PM6 PCBs with their ortho numbers.

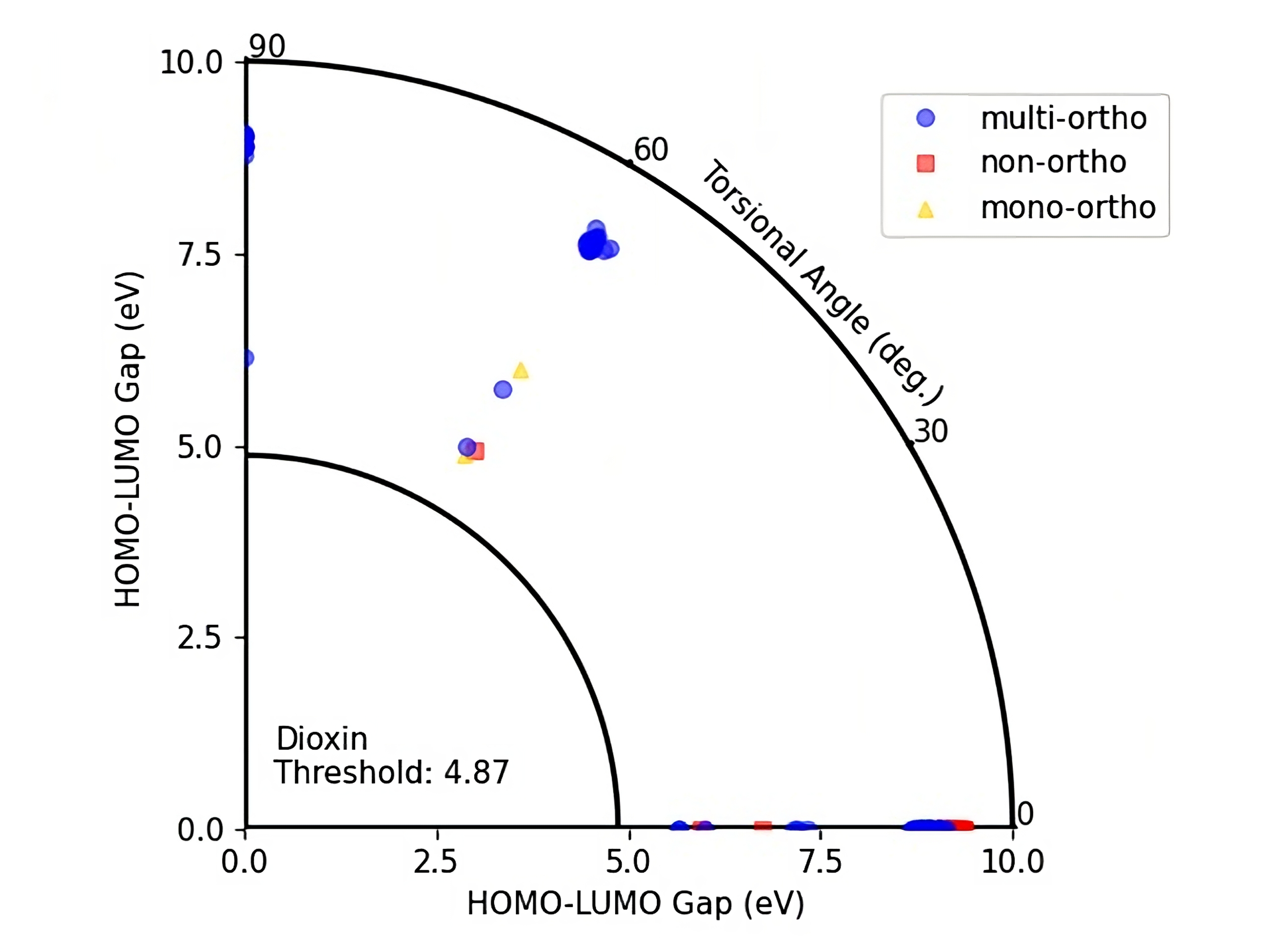
Figure 7: HOMO-LUMO Gap - Torsional angle representation of DelFTa predicted PCBs with their ortho numbers.

On these figures the radius of a quarter circle represents the HOMO-LUMO gap values and the angle of a point to the (0,0) coordinate represents the torsional angle. Blue circles represent multi-ortho, yellow triangles represents mono-ortho, and red squares represent non-ortho PCBs. The small quarter circle represents the Dioxin threshold which is equal to 4.87 eV.

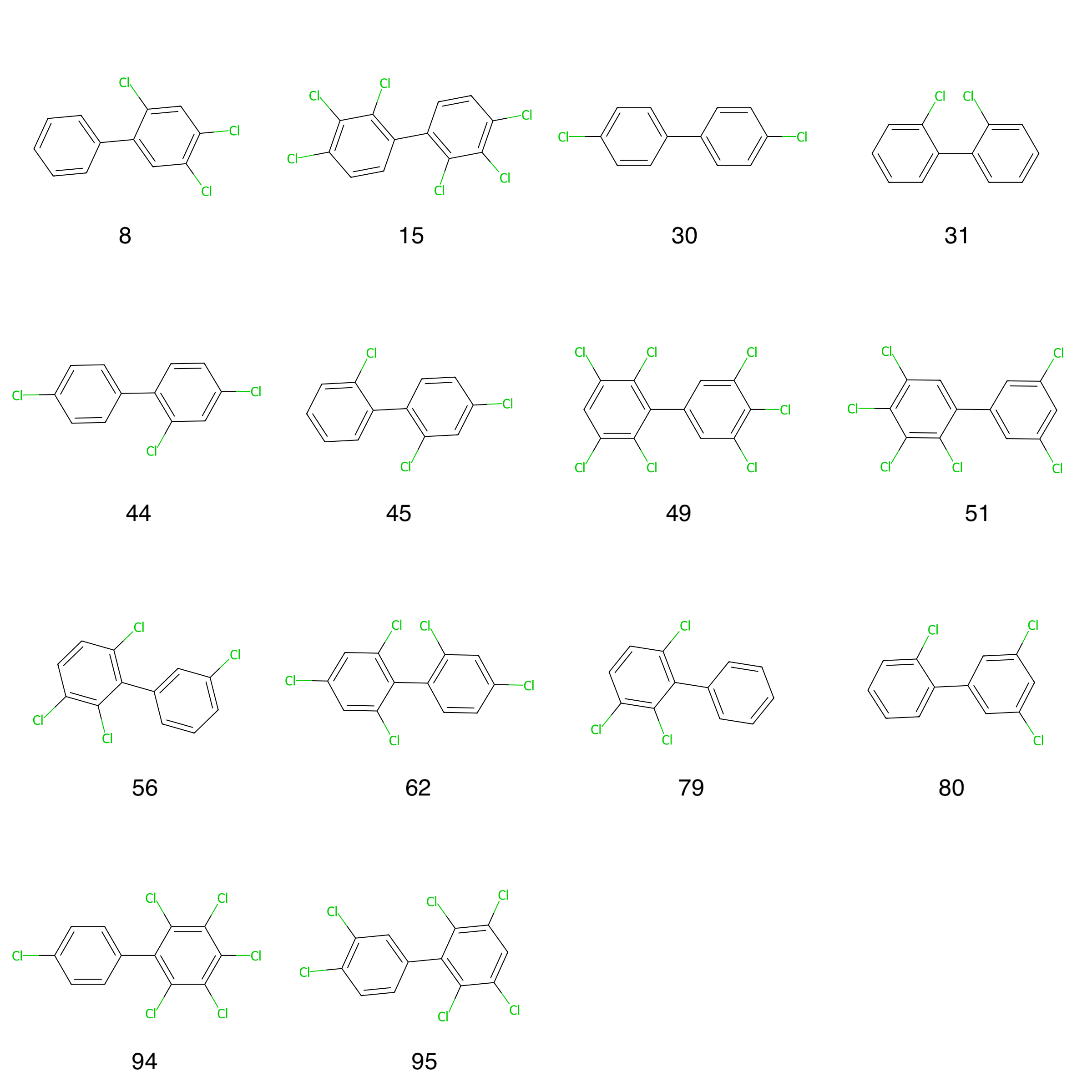
Figure 8: HOMO-LUMO gap outlier molecules with PCB indices.

Figure 8 depicts all outlier molecules and together with Table 1 we can differentiate between the outliers and see that most of the outliers are multi-ortho PCBs (9 out of 14), followed by non-ortho (3 out of 14) and mono-ortho (2 out of 14) PCBs. The outliers have been ordered by declining HOMO-LUMO gap difference values.

The highest HOMO-LUMO gap difference (3.1681) is observed for the multi-ortho PCB (PCB Index = 62) with a torsional angle of -90.12 degrees. This is the only PCB in the outlier set with a torsional angle around ±90 degrees. Most outlier PCBs exhibit torsional angles of around ±120 degrees (8 out of 14), followed by torsional angles of ±60 degrees (5 out of 14).

This analysis is valuable for re-training or fine-tuning purposes of the DelFTa model where more PCB structures with multi-ortho configuration and with a torsional angle of ±120 degrees could be added to the training set.

Table 1: HOMO-LUMO gap difference analysis between Delfta and PubchemQC PM6

We hope we showed you that the datasets we have integrated into our database can be of value for interesting machine learning studies with molecular quantum information. You are always welcome to reach out if you have any feedback, questions, ideas or even collaboration projects to push this kind of work and research further (contact (at) mqs [dot] dk).

References

[1] M. Nakata, T. Shimazaki, M. Hashimoto, and T. Maeda; J. Chem. Inf. Model. 2020, 60, 12, 5891–5899; https://doi.org/10.1021/acs.jcim.0c00740

[2] C. Isert, K. Atz, J. Jiménez-Luna & G. Schneider; Sci Data 9, 273 (2022); https://doi.org/10.1038/s41597-022-01390-7

[3] J. Marlowe and A. Puga; Comprehensive Toxicology (Second Edition) Volume 2, 2010, Pages 93-115; https://doi.org/10.1016/B978-0-08-046884-6.00207-4

[4] V. Rothhammer and F. J. Quintana; Nature Reviews Immunology volume 19, pages 184–197 (2019); https://doi.org/10.1038/s41577-019-0125-8

[5] J. Forrest, P. Bazylewski, R. Bauer, S. Hong, C. Y. Kim, J. P. Giesy, J. S. Khim and G. S. Chang; Front. Mar. Sci., 06 August 2014; https://doi.org/10.3389/fmars.2014.00031

[6] S. Safe; Environmental Health Perspectives 100, 1993; https://doi.org/10.1289/ehp.93100259

[7] W., X. Liu, H. Liu, Y. Wu, J. P. Giesy, H. Yu; Environmental Toxicology and Chemistry, Volume 29, Issue 3, March 2010; https://doi.org/10.1002/etc.70

[8] W. Yang, Y. Mu, J. P. Giesy, A. Zhang, H. Yu; Chemosphere Volume 75, Issue 9, May 2009, Pages 1159-1164; https://doi.org/10.1016/j.chemosphere.2009.02.047

[9] M. M. Lynam, M. Kuty, J. Damborsky, J. Koca, P. Adriaens; Environmental Toxicology and Chemistry, Volume 17, Issue 6, June 1998, Pages 988-997; https://doi.org/10.1002/etc.5620170603